GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回、アルマナックデータから3次元空間におけるGPS衛星の位置を求められましたので、そろそろ経度と緯度に関して触れておこうと思います。あえて、ふれてなかったところもありますが、経度と緯度はおくが深いです。
さて、次回あたりから、GPS衛星の位置を経度、緯度で表す方法をトライしてみようと思ってますが、その前に測地系について雑学を学んでおきましょう。
測地系という言葉は聞いたことはあるかとは思いますが、そもそも測地系って何?、正直、軌道計算を行う前までは、結構あいまいでした。定義自体は、
「地球上の位置を経緯度及び標高を用いる座標によって表すとき、前提とする条件」となっております。
つまり、測地系とは、経度、緯度を表現するために基とする条件なのです。
この測地系の条件として、3要素が上げられ、座標系、準拠楕円体、ジオイド面があります。
座標系は
中心を地球の重心を原点としたり、観測点を原点とするなど、座標の原点や、x、y、z軸の方向の定義に関わる部分です。
準拠楕円体は
地球は楕円ですが、その楕円の定義に関する部分です。
ジオイド面は
標高の基準の定義に関する部分です。
という感じですが、そもそも測地系って、なんで一つでないんだということになるのですが、今のように、技術が進歩してないときに、地図等をつくるために、いろいろな国が三角測量やら天体観測やらで、独自の測地系を作り上げたことが、理由にあるようです。
しかしながら、GPS等の発達によって、得られた情報による、正確な測地系の世界測地系へと変わりつつあります。
日本も、2002年に世界測地系に変わっています(思いのほか結構最近ですね)。とはいいつつも、例えば米国の世界測地系と日本の世界測地系とは違いがあります。
例えば、準拠楕円体は日本ではGRS80楕円体で、米国ではWGS84の楕円体だったりします。
米国の方だけ、「の」をいれましたが、このWGS84の中に、座標系やら準拠楕円体の定義が含まれてます。
しかしながら、ここで、一度つまづきました、なんで、日本はWGS84を採用しなかったのか、事実上、日本と米国の世界測地系にさほどの差異はないとのことですが、気になります。
ここら辺の回答というわけではないのですが、国土地理院のホームページにQ&Aがありそこを見るとなんとなくわかりました。
日本は世界測地系としてITRF系と呼ばれるものを採用しているそうなのですが、このQ&Aに採用した理由が以下のようになってました。
(1) 日本を含む国際協力で構築されている。我が国は、VLBI、GPS等の国際共同観測を通して、ITRF 系の構築に貢献しています。
(2) 高精度である。大量の宇宙測地観測結果から計算されるため高精度なものとなっています。
(3) 公開性が高い。一国により、又は軍事目的に構築されたものではないので、オープンなものとなっています。
なるほど、そういうことだったんですね。
政治的なところもあるようですね。
かなり大雑把でしが、ここらへんのネタはまたお話したいと思います。
さて、次回あたりから、GPS衛星の位置を経度、緯度で表す方法をトライしてみようと思ってますが、その前に測地系について雑学を学んでおきましょう。
測地系という言葉は聞いたことはあるかとは思いますが、そもそも測地系って何?、正直、軌道計算を行う前までは、結構あいまいでした。定義自体は、
「地球上の位置を経緯度及び標高を用いる座標によって表すとき、前提とする条件」となっております。
つまり、測地系とは、経度、緯度を表現するために基とする条件なのです。
この測地系の条件として、3要素が上げられ、座標系、準拠楕円体、ジオイド面があります。
座標系は
中心を地球の重心を原点としたり、観測点を原点とするなど、座標の原点や、x、y、z軸の方向の定義に関わる部分です。
準拠楕円体は
地球は楕円ですが、その楕円の定義に関する部分です。
ジオイド面は
標高の基準の定義に関する部分です。
という感じですが、そもそも測地系って、なんで一つでないんだということになるのですが、今のように、技術が進歩してないときに、地図等をつくるために、いろいろな国が三角測量やら天体観測やらで、独自の測地系を作り上げたことが、理由にあるようです。
しかしながら、GPS等の発達によって、得られた情報による、正確な測地系の世界測地系へと変わりつつあります。
日本も、2002年に世界測地系に変わっています(思いのほか結構最近ですね)。とはいいつつも、例えば米国の世界測地系と日本の世界測地系とは違いがあります。
例えば、準拠楕円体は日本ではGRS80楕円体で、米国ではWGS84の楕円体だったりします。
米国の方だけ、「の」をいれましたが、このWGS84の中に、座標系やら準拠楕円体の定義が含まれてます。
しかしながら、ここで、一度つまづきました、なんで、日本はWGS84を採用しなかったのか、事実上、日本と米国の世界測地系にさほどの差異はないとのことですが、気になります。
ここら辺の回答というわけではないのですが、国土地理院のホームページにQ&Aがありそこを見るとなんとなくわかりました。
日本は世界測地系としてITRF系と呼ばれるものを採用しているそうなのですが、このQ&Aに採用した理由が以下のようになってました。
(1) 日本を含む国際協力で構築されている。我が国は、VLBI、GPS等の国際共同観測を通して、ITRF 系の構築に貢献しています。
(2) 高精度である。大量の宇宙測地観測結果から計算されるため高精度なものとなっています。
(3) 公開性が高い。一国により、又は軍事目的に構築されたものではないので、オープンなものとなっています。
なるほど、そういうことだったんですね。
政治的なところもあるようですね。
かなり大雑把でしが、ここらへんのネタはまたお話したいと思います。
PR
いよいよ大ずめです。前回「アルマナックデータによるGPS衛星の位置計算其の2」で離心近点角Eをニュートン法により算出しました。今回は、クライマックスです。
さてさて、ここまでくれば、後は気が楽です。
まず、前に「航法メッセージによる GPS衛星の位置の求め方 其の3」に記載した、平面軌道上のGPS衛星位置(x',y')を求める公式を利用して、2次元面での、GPS衛星位置を求めます。
これはもう簡単ですよね。
x' = a*cos(E) - a*e
y' = a*sqrt(1-e2)*sine(E)
これで算出できます。ここで、お分かりだとは思いますが念のため、aは長半径、eは離心率、Eは離心近点角になります。
あとは、アルマナックデータおよび、前回求めた離心近点角Eを当てはめて解くだけです。解くと以下のようになります。
x' = -11120449.437278792
y' = -24439569.638433773
さてさて、最後に、上記2次元座標を3次元座標に変換してやりますがこれも、「航法メッセージによる GPS衛星の位置の求め方 其の3」で記述した、回転行列を利用します。
まずは、行列を解きます。すると、
X = x' * cos(Ωk) * cos(ω) - x' * sin(Ωk) * sin(ω) * cos(i)
- y' * cos(Ωk) * sin(ω) - y' * sin(Ωk) * cos(ω) * cos(i)
Y = x' * sin(Ωk) * cos(ω) + x' * cos(Ωk) * sin(ω) * cos(i)
- y' * sin(Ωk) * sin(ω) + y' * cos(Ωk) * cos(ω) * cos(i)
Z = x' * sin(Ωk) * sin(i) + y' * cos(Ωk) * sin(i)
となります。少々見にくいですが、こんな感じになります。ここでΩkは前回求めた、現在時刻による昇交点経度、i、ωはどちらもアルマナックデータより取得できそれぞれ、軌道傾斜角、近地点引数になります。考え方のおさらいをしますと。
「3次元の軌道面は、2次元の軌道面をz 軸回りにω 回転させ,続いてx 軸まわりにi,z 軸回りにΩ 回転させたものである」
でしたよね。
さて、実際にときますと、以下のようになります。
X = -26312458.28576335
Y = -3442369.7618006254
Z = 4094091.9850355694
どうでしたか?とうとう3次元空間における、GPS衛星の位置情報が求まりました。これは紛れも無い解です。しかしながら、GPS受信機という意味では不十分です。といいますのは、航法メッセージの中にはアルマナックデータだけでなく、エフェメリスデータというものが入っており、こちらのほうが正確な情報を持っているのですが、残念ながら、このやり方では、エフェメリスデータに含まれる補正データがうまく扱えません。よって、新たな角度、真近点角を利用した方法に置き換える必要があります。え!じゃー最初からそれをおしえろよ!と言われるかもしれませんが、概念的には今までの内容を理解していれば、問題ありませんし、入門としては、今回の方法から入ったほうが分かりやすいと思います。
機会があれば、エフェメリスデータによるGPS衛星の3次元空間上での位置の求め方を公開したいと思います。
さてさて、ここまでくれば、後は気が楽です。
まず、前に「航法メッセージによる GPS衛星の位置の求め方 其の3」に記載した、平面軌道上のGPS衛星位置(x',y')を求める公式を利用して、2次元面での、GPS衛星位置を求めます。
これはもう簡単ですよね。
x' = a*cos(E) - a*e
y' = a*sqrt(1-e2)*sine(E)
これで算出できます。ここで、お分かりだとは思いますが念のため、aは長半径、eは離心率、Eは離心近点角になります。
あとは、アルマナックデータおよび、前回求めた離心近点角Eを当てはめて解くだけです。解くと以下のようになります。
x' = -11120449.437278792
y' = -24439569.638433773
さてさて、最後に、上記2次元座標を3次元座標に変換してやりますがこれも、「航法メッセージによる GPS衛星の位置の求め方 其の3」で記述した、回転行列を利用します。
まずは、行列を解きます。すると、
X = x' * cos(Ωk) * cos(ω) - x' * sin(Ωk) * sin(ω) * cos(i)
- y' * cos(Ωk) * sin(ω) - y' * sin(Ωk) * cos(ω) * cos(i)
Y = x' * sin(Ωk) * cos(ω) + x' * cos(Ωk) * sin(ω) * cos(i)
- y' * sin(Ωk) * sin(ω) + y' * cos(Ωk) * cos(ω) * cos(i)
Z = x' * sin(Ωk) * sin(i) + y' * cos(Ωk) * sin(i)
となります。少々見にくいですが、こんな感じになります。ここでΩkは前回求めた、現在時刻による昇交点経度、i、ωはどちらもアルマナックデータより取得できそれぞれ、軌道傾斜角、近地点引数になります。考え方のおさらいをしますと。
「3次元の軌道面は、2次元の軌道面をz 軸回りにω 回転させ,続いてx 軸まわりにi,z 軸回りにΩ 回転させたものである」
でしたよね。
さて、実際にときますと、以下のようになります。
X = -26312458.28576335
Y = -3442369.7618006254
Z = 4094091.9850355694
どうでしたか?とうとう3次元空間における、GPS衛星の位置情報が求まりました。これは紛れも無い解です。しかしながら、GPS受信機という意味では不十分です。といいますのは、航法メッセージの中にはアルマナックデータだけでなく、エフェメリスデータというものが入っており、こちらのほうが正確な情報を持っているのですが、残念ながら、このやり方では、エフェメリスデータに含まれる補正データがうまく扱えません。よって、新たな角度、真近点角を利用した方法に置き換える必要があります。え!じゃー最初からそれをおしえろよ!と言われるかもしれませんが、概念的には今までの内容を理解していれば、問題ありませんし、入門としては、今回の方法から入ったほうが分かりやすいと思います。
機会があれば、エフェメリスデータによるGPS衛星の3次元空間上での位置の求め方を公開したいと思います。
前回「アルマナックデータによるGPS衛星の位置計算其の1」で、アルマナックデータからGPS衛星の位置を求めるための材料をそろえました。さて、今回は離心近点角をケプラーの方程式を利用して求めます。
すでに前回、平均近点角Mを求めていますから、簡単に求まるようにも思えますが、残念ながら、すんなりとは求まりません。理由としては、非線形だからです。したがって、ニュートン法を用いて、近似解を求めます。尚、ここではニュートン法の説明はしませんのでがんばってググってください。
さてまず、ケプラーの方程式をニュートン法にて離心近点角Eを解くため以下のように設定します。
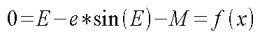
数式1
次に、以下の漸化式に数式1をあてはめます。
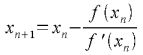
数式2
数式1を数式2に当てはめると次式が得られます。
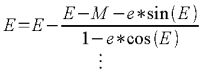
数式3
ここで、初期E0 = M = 73.40211084258863として、数式3を繰り返し演算していけば、値が収束します。永久に計算をし続けるわけにもいけませんので、前後のEの値を比較して、十分差が小さければ、そのEを利用します。
尚、ニュートン法では、解になるべく近い初期値を設定しないと、発散したり、なかなか、解が求まらないという自体になりかねませんが、Mを初期値にしておけば、この場合問題ありません。
さて、実際にEを求めるとE = 73.40125940150486 となります。
ニュートン法は軌道計算にくらべたら、まだ理解しやすい方なので、ググって是非理解してください。解析には欠かせないアイテムの一つです。
では次回で最終章といたしましょう。
すでに前回、平均近点角Mを求めていますから、簡単に求まるようにも思えますが、残念ながら、すんなりとは求まりません。理由としては、非線形だからです。したがって、ニュートン法を用いて、近似解を求めます。尚、ここではニュートン法の説明はしませんのでがんばってググってください。
さてまず、ケプラーの方程式をニュートン法にて離心近点角Eを解くため以下のように設定します。
数式1
次に、以下の漸化式に数式1をあてはめます。
数式2
数式1を数式2に当てはめると次式が得られます。
数式3
ここで、初期E0 = M = 73.40211084258863として、数式3を繰り返し演算していけば、値が収束します。永久に計算をし続けるわけにもいけませんので、前後のEの値を比較して、十分差が小さければ、そのEを利用します。
尚、ニュートン法では、解になるべく近い初期値を設定しないと、発散したり、なかなか、解が求まらないという自体になりかねませんが、Mを初期値にしておけば、この場合問題ありません。
さて、実際にEを求めるとE = 73.40125940150486 となります。
ニュートン法は軌道計算にくらべたら、まだ理解しやすい方なので、ググって是非理解してください。解析には欠かせないアイテムの一つです。
では次回で最終章といたしましょう。
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

