GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
ちょっと今回は番外編です。「GT-730F/Lのログデータで何かやってみる其の5」で、経度、緯度で示される点、2点から、北を進行方向として、どの程度のずれがあるか、平面三角法により角度を求めました。
しかしながら、地球は実際は球体です。ですので、今回は球面三角法を用いて、角度を求めてみます。といっても、つっこんだことはしませんが。
球面三角法は、天文学等で利用されてきたようで、技術の発達した現在は、行列を利用した座標変換が主流らしいです。そもそもどうやって、利用されてきたのかがわからないのでぴんとこないですが、座標変換というところから考えて、"測地系"に関わるところなのでしょうか。
ひとまず、ここはおいといて。
まず、平面三角法との違いは、ウィキの内容でいくと、
「平面上の三角法との最大の違いは、辺の大きさが長さではなく球の中心角によって表されることである。」
となっております。ちょっと分かりにくいので、以下の図を見てください。
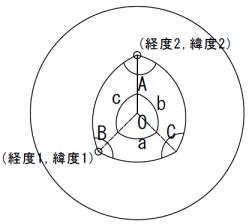
図1
図1は地球と思ってください。地球の中心をOとし、A、B、Cは地球表面のとあるポイントとします。そして、この4点を線で繋いだ時にできる角度、A、B、C、a、b、cの6角度を図1は表しています。実は、球面三角法は、この6角度により、表現できる公式なのです。
ウィキの図だと、素人がみると、a、b、cが球の中心角でなく、単純に辺の長さに見えてしまうので、ウィキを参照するときは注意してください。どうでもいいことですが、エクセルでの作図は限界がきたので、とうとうCAD(フリーのものですが)を使ってしまいました。慣れていないのでうまく作図できていないですが、CADは便利だとあらためて実感しました。
さて、球面三角法も平面三角法に似せて、余弦定理や、正弦定理が存在しますが、ここでは説明は省きます。
ここで、GPSロガーから取得した、経度、緯度であらわされる点、2点を図1のように仮にします。そして、Cの角度を90度になるように設定します(Cの経度をAの経度,Cの緯度をBの緯度とすれば必然的に90度になりますが、公式上はCを90度とするならCは無視できます)。ここで求めたい角度はBとなり。以下の公式を利用すれば、角度Bを求めることができます。
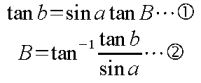
数式1
①の公式より、逆三角関数から、②式が得られ、角度Bを求めることができます。
Cの角度を90度とすると、公式は結構単純になります。
公式の証明はしませんが、この場合は、なんとなく直感でわかるんでないでしょうか。
ここで、bは図1より、b = 緯度2 - 緯度1、a = 経度2 - 経度1となります。
球面三角法の場合ですと、こんな感じで、角度の計算ができます。
尚、お気づきの方もいるかもしれませんが、平面の場合は三角形の内角の和は180度でしたが、球面の場合は180度を越えます。
ただし、これは、図1のように、大きい三点をとったとき、顕著に180度を越えたことがわかりますが、地球の大きさに対して、A、B間が数百メートル程度では、平面の時とほとんど変わらないです。また、実際には、地球は楕円かつ、山あり谷ありで、まだまだ考慮すべきところは多いです。
また、とりあえず、角度は求めたものの、この角度を利用するには、地図の図法に応じた変換も必要で、素人はおとなしく平面三角法で遊んでいたほうがいいかもしれません。
では、今日はここまで。
しかしながら、地球は実際は球体です。ですので、今回は球面三角法を用いて、角度を求めてみます。といっても、つっこんだことはしませんが。
球面三角法は、天文学等で利用されてきたようで、技術の発達した現在は、行列を利用した座標変換が主流らしいです。そもそもどうやって、利用されてきたのかがわからないのでぴんとこないですが、座標変換というところから考えて、"測地系"に関わるところなのでしょうか。
ひとまず、ここはおいといて。
まず、平面三角法との違いは、ウィキの内容でいくと、
「平面上の三角法との最大の違いは、辺の大きさが長さではなく球の中心角によって表されることである。」
となっております。ちょっと分かりにくいので、以下の図を見てください。
図1
図1は地球と思ってください。地球の中心をOとし、A、B、Cは地球表面のとあるポイントとします。そして、この4点を線で繋いだ時にできる角度、A、B、C、a、b、cの6角度を図1は表しています。実は、球面三角法は、この6角度により、表現できる公式なのです。
ウィキの図だと、素人がみると、a、b、cが球の中心角でなく、単純に辺の長さに見えてしまうので、ウィキを参照するときは注意してください。どうでもいいことですが、エクセルでの作図は限界がきたので、とうとうCAD(フリーのものですが)を使ってしまいました。慣れていないのでうまく作図できていないですが、CADは便利だとあらためて実感しました。
さて、球面三角法も平面三角法に似せて、余弦定理や、正弦定理が存在しますが、ここでは説明は省きます。
ここで、GPSロガーから取得した、経度、緯度であらわされる点、2点を図1のように仮にします。そして、Cの角度を90度になるように設定します(Cの経度をAの経度,Cの緯度をBの緯度とすれば必然的に90度になりますが、公式上はCを90度とするならCは無視できます)。ここで求めたい角度はBとなり。以下の公式を利用すれば、角度Bを求めることができます。
数式1
①の公式より、逆三角関数から、②式が得られ、角度Bを求めることができます。
Cの角度を90度とすると、公式は結構単純になります。
公式の証明はしませんが、この場合は、なんとなく直感でわかるんでないでしょうか。
ここで、bは図1より、b = 緯度2 - 緯度1、a = 経度2 - 経度1となります。
球面三角法の場合ですと、こんな感じで、角度の計算ができます。
尚、お気づきの方もいるかもしれませんが、平面の場合は三角形の内角の和は180度でしたが、球面の場合は180度を越えます。
ただし、これは、図1のように、大きい三点をとったとき、顕著に180度を越えたことがわかりますが、地球の大きさに対して、A、B間が数百メートル程度では、平面の時とほとんど変わらないです。また、実際には、地球は楕円かつ、山あり谷ありで、まだまだ考慮すべきところは多いです。
また、とりあえず、角度は求めたものの、この角度を利用するには、地図の図法に応じた変換も必要で、素人はおとなしく平面三角法で遊んでいたほうがいいかもしれません。
では、今日はここまで。
PR
前回「GT-730F/Lのログデータで何かやってみる其の8」の続きです。
前回、Waypointの設定もできるようにはしましたが、地図をクリックすると、即座に半径100mの円が描画されてしまう等、結構、設定がめんどくさいので少し改善してみます。
とりあえず動きてきには以下のようにしてみます。
1. VB上に、チェックボックスを配置し、そこにチェックが入っている間だけ、WayPointが指定できる。通常は地図の移動のみ。
2. 最初マップにクリックすると、Waypointエリアの中心が指定され、次にマップをクリックすると、最初の経度緯度と次の経度緯度との距離をエリアの半径とし、円が描画される。
3. さらにマップをクリックすると、前回の円を消去し、新たなWaypointエリアの中心が指定される。これ以降の動作は同じ。
上記のような感じにしてみます。これで、Waypointエリア半径も指定できます。
なにやら、めんどくさそうですが、意外に、簡単にできます。ほとんどが、地図のAPIの改造になります。
2点間の距離はこのブログでは同じみの、三平方の定理で、以下のようにします。
Math.sqrt(Math.pow(((現在経度 - 前の経度) / 0.000009),2) + Math.pow(((現在の緯度 - 前の緯度) / 0.000009),2))
とりあえず、これで、コーディングしてもいいのですが、電子国土では、地名検索機能もあるので、これも導入してみます。正直、サンプルも用意されており、そのサンプルをフレームタグで呼び出すようにすれば、すぐに利用できるようになってます。
これでWaypoint指定も結構楽になりそうです。
完成イメージは以下の通りです。
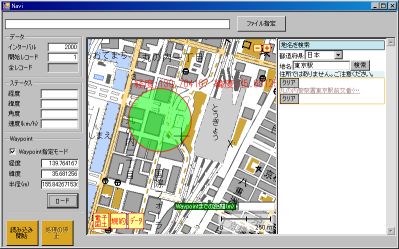
少々レイアウトも変更してます。
では今日はここまで。
前回、Waypointの設定もできるようにはしましたが、地図をクリックすると、即座に半径100mの円が描画されてしまう等、結構、設定がめんどくさいので少し改善してみます。
とりあえず動きてきには以下のようにしてみます。
1. VB上に、チェックボックスを配置し、そこにチェックが入っている間だけ、WayPointが指定できる。通常は地図の移動のみ。
2. 最初マップにクリックすると、Waypointエリアの中心が指定され、次にマップをクリックすると、最初の経度緯度と次の経度緯度との距離をエリアの半径とし、円が描画される。
3. さらにマップをクリックすると、前回の円を消去し、新たなWaypointエリアの中心が指定される。これ以降の動作は同じ。
上記のような感じにしてみます。これで、Waypointエリア半径も指定できます。
なにやら、めんどくさそうですが、意外に、簡単にできます。ほとんどが、地図のAPIの改造になります。
2点間の距離はこのブログでは同じみの、三平方の定理で、以下のようにします。
Math.sqrt(Math.pow(((現在経度 - 前の経度) / 0.000009),2) + Math.pow(((現在の緯度 - 前の緯度) / 0.000009),2))
とりあえず、これで、コーディングしてもいいのですが、電子国土では、地名検索機能もあるので、これも導入してみます。正直、サンプルも用意されており、そのサンプルをフレームタグで呼び出すようにすれば、すぐに利用できるようになってます。
これでWaypoint指定も結構楽になりそうです。
完成イメージは以下の通りです。
少々レイアウトも変更してます。
では今日はここまで。
前回「GT-730F/Lのログデータで何かやってみる其の7」の続きです。カーナビモドキに、一箇所だけですが、ウェイポイント設定ができるようになりましたので、早速実験してみることにします。
ひとまず今回は、すでに、ブログにも何度も記載してますが、名古屋方面から、北陸に行った時のログデータを利用し、検証してみます。
まずは、ウェイポイントですが、適当に、経度 136.9486、緯度 35.69839にとり、十分はなれた、ログから開始させ、ウェイポイントの半径100mの円に入るか確認してみます。
すると、残念ながら、半径100mにははいらず、もっとも近かったのが、以下の画面に示す通りです。実際の位置は十字のところです。
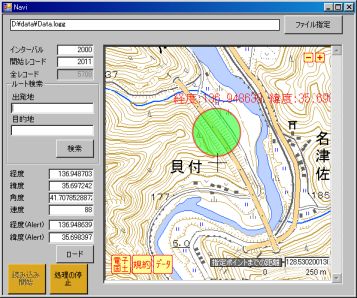
右下のほうに「指定ポイントまでの距離」とでていますが、ウェイポイントと現在距離が、128m付近まではいきましたが、この後、いっきにぶっとびます。
そもそも、北陸道は、トンネルや山も多いので上手くGPSが測位できていないこともよくわかります。
同様に、本ログで無作為にウェイポイントを設定し、試しましたが、エリア内に入るのは結構少なかったです。
少々、考察してみましょう。データのログから、今回、検証対象とした、区間の車の速度は平均90km/h程度です。そして、GPS測位の間隔は5秒間隔になっています。
ここで、90km/hで5秒間走ったら何mになるかこれは125mになります、つまり、ウェイポイントは直径200m程度になっていますから、本来、125m間隔で測位ができているならば、エリアに入るはずですが、そうでなかったのは、前述のとおり、トンネル等の問題で、上手く測位ができなかったからと推測されます。
よって、こういった、トンネルが多いところでは、ウェイポイントのエリアを広くしないと上手くいかないということがよく分かります。
この調子で今後もいろいろ検証していきます。
ひとまず今回は、すでに、ブログにも何度も記載してますが、名古屋方面から、北陸に行った時のログデータを利用し、検証してみます。
まずは、ウェイポイントですが、適当に、経度 136.9486、緯度 35.69839にとり、十分はなれた、ログから開始させ、ウェイポイントの半径100mの円に入るか確認してみます。
すると、残念ながら、半径100mにははいらず、もっとも近かったのが、以下の画面に示す通りです。実際の位置は十字のところです。
右下のほうに「指定ポイントまでの距離」とでていますが、ウェイポイントと現在距離が、128m付近まではいきましたが、この後、いっきにぶっとびます。
そもそも、北陸道は、トンネルや山も多いので上手くGPSが測位できていないこともよくわかります。
同様に、本ログで無作為にウェイポイントを設定し、試しましたが、エリア内に入るのは結構少なかったです。
少々、考察してみましょう。データのログから、今回、検証対象とした、区間の車の速度は平均90km/h程度です。そして、GPS測位の間隔は5秒間隔になっています。
ここで、90km/hで5秒間走ったら何mになるかこれは125mになります、つまり、ウェイポイントは直径200m程度になっていますから、本来、125m間隔で測位ができているならば、エリアに入るはずですが、そうでなかったのは、前述のとおり、トンネル等の問題で、上手く測位ができなかったからと推測されます。
よって、こういった、トンネルが多いところでは、ウェイポイントのエリアを広くしないと上手くいかないということがよく分かります。
この調子で今後もいろいろ検証していきます。
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

