GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回「アルマナックデータによるGPS衛星の位置計算其の1」で、アルマナックデータからGPS衛星の位置を求めるための材料をそろえました。さて、今回は離心近点角をケプラーの方程式を利用して求めます。
すでに前回、平均近点角Mを求めていますから、簡単に求まるようにも思えますが、残念ながら、すんなりとは求まりません。理由としては、非線形だからです。したがって、ニュートン法を用いて、近似解を求めます。尚、ここではニュートン法の説明はしませんのでがんばってググってください。
さてまず、ケプラーの方程式をニュートン法にて離心近点角Eを解くため以下のように設定します。
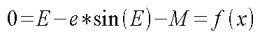
数式1
次に、以下の漸化式に数式1をあてはめます。
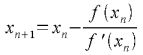
数式2
数式1を数式2に当てはめると次式が得られます。
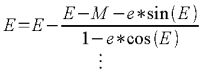
数式3
ここで、初期E0 = M = 73.40211084258863として、数式3を繰り返し演算していけば、値が収束します。永久に計算をし続けるわけにもいけませんので、前後のEの値を比較して、十分差が小さければ、そのEを利用します。
尚、ニュートン法では、解になるべく近い初期値を設定しないと、発散したり、なかなか、解が求まらないという自体になりかねませんが、Mを初期値にしておけば、この場合問題ありません。
さて、実際にEを求めるとE = 73.40125940150486 となります。
ニュートン法は軌道計算にくらべたら、まだ理解しやすい方なので、ググって是非理解してください。解析には欠かせないアイテムの一つです。
では次回で最終章といたしましょう。
すでに前回、平均近点角Mを求めていますから、簡単に求まるようにも思えますが、残念ながら、すんなりとは求まりません。理由としては、非線形だからです。したがって、ニュートン法を用いて、近似解を求めます。尚、ここではニュートン法の説明はしませんのでがんばってググってください。
さてまず、ケプラーの方程式をニュートン法にて離心近点角Eを解くため以下のように設定します。
数式1
次に、以下の漸化式に数式1をあてはめます。
数式2
数式1を数式2に当てはめると次式が得られます。
数式3
ここで、初期E0 = M = 73.40211084258863として、数式3を繰り返し演算していけば、値が収束します。永久に計算をし続けるわけにもいけませんので、前後のEの値を比較して、十分差が小さければ、そのEを利用します。
尚、ニュートン法では、解になるべく近い初期値を設定しないと、発散したり、なかなか、解が求まらないという自体になりかねませんが、Mを初期値にしておけば、この場合問題ありません。
さて、実際にEを求めるとE = 73.40125940150486 となります。
ニュートン法は軌道計算にくらべたら、まだ理解しやすい方なので、ググって是非理解してください。解析には欠かせないアイテムの一つです。
では次回で最終章といたしましょう。
PR
この記事にコメントする
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

