GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回の「WGS84測地系モドキによるGPS衛星の経度緯度の求め方其の2」の続きです。前回、座標系の変換を行いましたので、今回は、地球を楕円でなく球とみなして、いよいよ経度と緯度を求めてみます。
正直、球とみなせば、比較的単純に経度と緯度が求まります。まず、地球中心からGPS衛星までの距離をr、経度をλ、緯度をΦとすると、前回求めた、座標は以下のように表すことができます。
XECEF = r*cosΦ*cosλ
YECEF = r*cosΦ*sinλ
ZECEF = r*sinΦ
これはいたって単純です。分からない人は、以前、お話したように、一度、地球とGPS衛星の絵を描いてみて、経度、緯度をベースに
さ~いん、こさ~いん
と指でなぞってみるとよくわかると思います。
さて、ここで求めたい値はΦとλです。まずは、経度λを求めて見ましょう。
まず、以下の式をみてください。
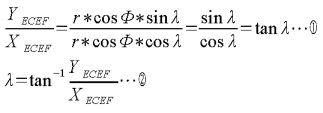
数式1
このように、まずはYECEF/XECEFが、tanλになることを利用し数式1の②でその逆数をとることで、経度λが求まります。注意せねばならないのは、アークタンジェントの結果は -π/2からπ/2の範囲でしか答えがえられませんので、求まった答えの象限に応じ加工してやる必要があるのですが、javascript等の言語ではatan2(Y,X)という感じで-πからπの範囲に変換してくれる関数がありますので、これを利用すると便利です。
次に、緯度Φを求めて見ましょう。地球を球と考えた場合、緯度も同様に求めることができます。
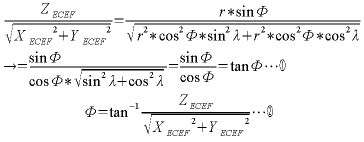
数式2
sqrt(XECEF2+YECEF2)の部分は単純に3平方の定理で、ZECEFに対応するもう1辺を求めているだけです。あとは経度の時と同様に計算するだけです。いやはや、中学や高校のころは、三角関数がこんなところで利用できるとは思ってもみませんでした。
さあいかがでしたでしょうか?これで、経度緯度が求まったわけですが、実際には地球は楕円です。ですから、今回求めた方法よりも、計算は複雑になります。しかしながら、考え方や式の成分は今回と同じですから、とっつきやすいとは思います。
とはいえ、近似式を利用するなど、式自体を理解するには、軌道計算同様、時間を要します。
いずれにしましても、基本をまずはしっかり押さえておくことが大事です。
また、機会があれば、WGS84 準拠楕円体を考慮した、経度緯度の求め方も公開します。そのまえに、エフェメリスデータによる、GPSの位置計算もしたいところです。
正直、球とみなせば、比較的単純に経度と緯度が求まります。まず、地球中心からGPS衛星までの距離をr、経度をλ、緯度をΦとすると、前回求めた、座標は以下のように表すことができます。
XECEF = r*cosΦ*cosλ
YECEF = r*cosΦ*sinλ
ZECEF = r*sinΦ
これはいたって単純です。分からない人は、以前、お話したように、一度、地球とGPS衛星の絵を描いてみて、経度、緯度をベースに
さ~いん、こさ~いん
と指でなぞってみるとよくわかると思います。
さて、ここで求めたい値はΦとλです。まずは、経度λを求めて見ましょう。
まず、以下の式をみてください。
数式1
このように、まずはYECEF/XECEFが、tanλになることを利用し数式1の②でその逆数をとることで、経度λが求まります。注意せねばならないのは、アークタンジェントの結果は -π/2からπ/2の範囲でしか答えがえられませんので、求まった答えの象限に応じ加工してやる必要があるのですが、javascript等の言語ではatan2(Y,X)という感じで-πからπの範囲に変換してくれる関数がありますので、これを利用すると便利です。
次に、緯度Φを求めて見ましょう。地球を球と考えた場合、緯度も同様に求めることができます。
数式2
sqrt(XECEF2+YECEF2)の部分は単純に3平方の定理で、ZECEFに対応するもう1辺を求めているだけです。あとは経度の時と同様に計算するだけです。いやはや、中学や高校のころは、三角関数がこんなところで利用できるとは思ってもみませんでした。
さあいかがでしたでしょうか?これで、経度緯度が求まったわけですが、実際には地球は楕円です。ですから、今回求めた方法よりも、計算は複雑になります。しかしながら、考え方や式の成分は今回と同じですから、とっつきやすいとは思います。
とはいえ、近似式を利用するなど、式自体を理解するには、軌道計算同様、時間を要します。
いずれにしましても、基本をまずはしっかり押さえておくことが大事です。
また、機会があれば、WGS84 準拠楕円体を考慮した、経度緯度の求め方も公開します。そのまえに、エフェメリスデータによる、GPSの位置計算もしたいところです。
PR
この記事にコメントする
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

