GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回の「WGS84測地系モドキによるGPS衛星の経度緯度の求め方其の2」の続きです。前回、座標系の変換を行いましたので、今回は、地球を楕円でなく球とみなして、いよいよ経度と緯度を求めてみます。
正直、球とみなせば、比較的単純に経度と緯度が求まります。まず、地球中心からGPS衛星までの距離をr、経度をλ、緯度をΦとすると、前回求めた、座標は以下のように表すことができます。
XECEF = r*cosΦ*cosλ
YECEF = r*cosΦ*sinλ
ZECEF = r*sinΦ
これはいたって単純です。分からない人は、以前、お話したように、一度、地球とGPS衛星の絵を描いてみて、経度、緯度をベースに
さ~いん、こさ~いん
と指でなぞってみるとよくわかると思います。
さて、ここで求めたい値はΦとλです。まずは、経度λを求めて見ましょう。
まず、以下の式をみてください。
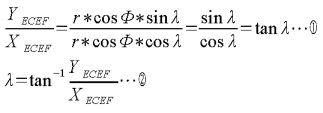
数式1
このように、まずはYECEF/XECEFが、tanλになることを利用し数式1の②でその逆数をとることで、経度λが求まります。注意せねばならないのは、アークタンジェントの結果は -π/2からπ/2の範囲でしか答えがえられませんので、求まった答えの象限に応じ加工してやる必要があるのですが、javascript等の言語ではatan2(Y,X)という感じで-πからπの範囲に変換してくれる関数がありますので、これを利用すると便利です。
次に、緯度Φを求めて見ましょう。地球を球と考えた場合、緯度も同様に求めることができます。
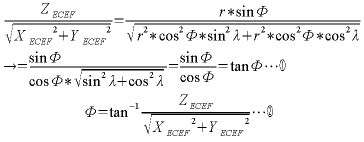
数式2
sqrt(XECEF2+YECEF2)の部分は単純に3平方の定理で、ZECEFに対応するもう1辺を求めているだけです。あとは経度の時と同様に計算するだけです。いやはや、中学や高校のころは、三角関数がこんなところで利用できるとは思ってもみませんでした。
さあいかがでしたでしょうか?これで、経度緯度が求まったわけですが、実際には地球は楕円です。ですから、今回求めた方法よりも、計算は複雑になります。しかしながら、考え方や式の成分は今回と同じですから、とっつきやすいとは思います。
とはいえ、近似式を利用するなど、式自体を理解するには、軌道計算同様、時間を要します。
いずれにしましても、基本をまずはしっかり押さえておくことが大事です。
また、機会があれば、WGS84 準拠楕円体を考慮した、経度緯度の求め方も公開します。そのまえに、エフェメリスデータによる、GPSの位置計算もしたいところです。
正直、球とみなせば、比較的単純に経度と緯度が求まります。まず、地球中心からGPS衛星までの距離をr、経度をλ、緯度をΦとすると、前回求めた、座標は以下のように表すことができます。
XECEF = r*cosΦ*cosλ
YECEF = r*cosΦ*sinλ
ZECEF = r*sinΦ
これはいたって単純です。分からない人は、以前、お話したように、一度、地球とGPS衛星の絵を描いてみて、経度、緯度をベースに
さ~いん、こさ~いん
と指でなぞってみるとよくわかると思います。
さて、ここで求めたい値はΦとλです。まずは、経度λを求めて見ましょう。
まず、以下の式をみてください。
数式1
このように、まずはYECEF/XECEFが、tanλになることを利用し数式1の②でその逆数をとることで、経度λが求まります。注意せねばならないのは、アークタンジェントの結果は -π/2からπ/2の範囲でしか答えがえられませんので、求まった答えの象限に応じ加工してやる必要があるのですが、javascript等の言語ではatan2(Y,X)という感じで-πからπの範囲に変換してくれる関数がありますので、これを利用すると便利です。
次に、緯度Φを求めて見ましょう。地球を球と考えた場合、緯度も同様に求めることができます。
数式2
sqrt(XECEF2+YECEF2)の部分は単純に3平方の定理で、ZECEFに対応するもう1辺を求めているだけです。あとは経度の時と同様に計算するだけです。いやはや、中学や高校のころは、三角関数がこんなところで利用できるとは思ってもみませんでした。
さあいかがでしたでしょうか?これで、経度緯度が求まったわけですが、実際には地球は楕円です。ですから、今回求めた方法よりも、計算は複雑になります。しかしながら、考え方や式の成分は今回と同じですから、とっつきやすいとは思います。
とはいえ、近似式を利用するなど、式自体を理解するには、軌道計算同様、時間を要します。
いずれにしましても、基本をまずはしっかり押さえておくことが大事です。
また、機会があれば、WGS84 準拠楕円体を考慮した、経度緯度の求め方も公開します。そのまえに、エフェメリスデータによる、GPSの位置計算もしたいところです。
PR
今回は、「WGS84測地系モドキによるGPS衛星の経度緯度の求め方其の1」でお話したWGS84測地系の座標系に変換してみます。
実は、ここの概念が、本件では一番分かりにくい話になります。
まず「アルマナックデータによるGPS衛星の位置計算其の3」で求めたGPS位置(X,Y,Z)の座標系はそもそも何だったのかからお話しますと、地球中心慣性ECI(Earth-Centered Inertial)座標系というものであり、座標原点が地球の質量中心にあり、ニュートン力学の原理基盤となっている座標系です。まずこの時点で挫折しそうですねえ。
次に、ちょっとすっとばして、上記の座標系を今回の主題であるWGS84測地系の座標系に変換するわけですが、この座標系は地球中心地球固定ECEF(Earth-Centered Earth-Fixed)座標系と呼ばれ、GPS 受信機などの位置を記述するために、地球の自転と共に回転する座標系です。
どうでしょうか?なんとなくわかってきましたか?まず、単純に言いますと、今回おこなう作業は地球の自転を考慮し座標系を回転させてやるのです。
ええ!じゃあ今までは、そうじゃなかったの?と思う人もいるかもしれませんが、そうじゃなかったのです。物事には順序というものがあります。まあ、がんばってついてきてください。
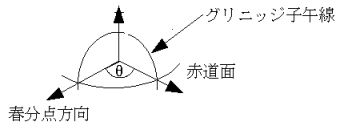
図1
まずは図1をみてください。以前、x軸方向の座標を決定する際、春分点方向という言葉を使いました。実は、その時はさほど重要ではなかったのでさらっと流したのですが、実は、今回の座標変換の種を明かせば、この春分点方向から、地球の自転軸で回転させ、地球のグリニッジ子午線に合わせるという行為なのです。
グリニッジ子午線は経度0ですので、ここにあわせるのは緯度、経度を求める上では明快だと思います。しかしながら、そもそも春分点とは何か?という話なのですが、これは
「黄道と天の赤道との2つの交点(分点)のうち、黄道が南から北へ交わる方の点(昇交点)のこと。この点が赤経0 度かつ黄経0度であり、この点を太陽が通過する瞬間が春分となる。」
というものです。ますます意味不明ですよね。とりあえず、天文学的に、星の位置を示すための基準点とでも思ってください。
ここで、図1のθはグリニッジ恒星時とよばれている角度になるのですが、これを求めるためGPS衛星の場合は、航法メッセージにも定義されている、地球の平均自転速度ωE=7,292,115.1467E-11を利用します。
実際にθを求めるには、GPS週の最初を、春分点方向 = グリニッジ子午線とし、そこから、現在時刻までの自転による角度のずれをωEを利用し求めるだけです。計算的には以下の通り。
θ = ωE * GPS週の最初から現在までの秒数
すでにおわかりでしょうが、GPS週はアルマナックデータより取得可能です。尚、グリニッジ恒星時も奥が深いのでここでは深く突っ込みません。
ここでθがもとまりましたので、すでに求めている。GPS衛星位置(X,Y,Z)を回転行列を用いて、θ回転させてみましょう。
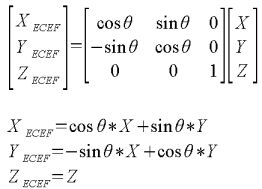
数式1
これはいたって明快ですよね。正直、すごく単純に記載しましたが、天文学も奥が深く、簡単に語れるものではありませんが、計算はこんな感じです。
今日はここまで。
実は、ここの概念が、本件では一番分かりにくい話になります。
まず「アルマナックデータによるGPS衛星の位置計算其の3」で求めたGPS位置(X,Y,Z)の座標系はそもそも何だったのかからお話しますと、地球中心慣性ECI(Earth-Centered Inertial)座標系というものであり、座標原点が地球の質量中心にあり、ニュートン力学の原理基盤となっている座標系です。まずこの時点で挫折しそうですねえ。
次に、ちょっとすっとばして、上記の座標系を今回の主題であるWGS84測地系の座標系に変換するわけですが、この座標系は地球中心地球固定ECEF(Earth-Centered Earth-Fixed)座標系と呼ばれ、GPS 受信機などの位置を記述するために、地球の自転と共に回転する座標系です。
どうでしょうか?なんとなくわかってきましたか?まず、単純に言いますと、今回おこなう作業は地球の自転を考慮し座標系を回転させてやるのです。
ええ!じゃあ今までは、そうじゃなかったの?と思う人もいるかもしれませんが、そうじゃなかったのです。物事には順序というものがあります。まあ、がんばってついてきてください。
図1
まずは図1をみてください。以前、x軸方向の座標を決定する際、春分点方向という言葉を使いました。実は、その時はさほど重要ではなかったのでさらっと流したのですが、実は、今回の座標変換の種を明かせば、この春分点方向から、地球の自転軸で回転させ、地球のグリニッジ子午線に合わせるという行為なのです。
グリニッジ子午線は経度0ですので、ここにあわせるのは緯度、経度を求める上では明快だと思います。しかしながら、そもそも春分点とは何か?という話なのですが、これは
「黄道と天の赤道との2つの交点(分点)のうち、黄道が南から北へ交わる方の点(昇交点)のこと。この点が赤経0 度かつ黄経0度であり、この点を太陽が通過する瞬間が春分となる。」
というものです。ますます意味不明ですよね。とりあえず、天文学的に、星の位置を示すための基準点とでも思ってください。
ここで、図1のθはグリニッジ恒星時とよばれている角度になるのですが、これを求めるためGPS衛星の場合は、航法メッセージにも定義されている、地球の平均自転速度ωE=7,292,115.1467E-11を利用します。
実際にθを求めるには、GPS週の最初を、春分点方向 = グリニッジ子午線とし、そこから、現在時刻までの自転による角度のずれをωEを利用し求めるだけです。計算的には以下の通り。
θ = ωE * GPS週の最初から現在までの秒数
すでにおわかりでしょうが、GPS週はアルマナックデータより取得可能です。尚、グリニッジ恒星時も奥が深いのでここでは深く突っ込みません。
ここでθがもとまりましたので、すでに求めている。GPS衛星位置(X,Y,Z)を回転行列を用いて、θ回転させてみましょう。
数式1
これはいたって明快ですよね。正直、すごく単純に記載しましたが、天文学も奥が深く、簡単に語れるものではありませんが、計算はこんな感じです。
今日はここまで。
前回、「アルマナックデータによるGPS衛星の位置計算其の3」で3次元空間上でのアルマナックによるGPS衛星の位置(X,Y,Z)の求め方を掲載しました。今回は公約通り、これを経度緯度で表現する方法を一緒にまなんでいきましょう。これがわかれば、地球上のどのあたりの上空にGPS衛星があるかわかります。
尚、すでに、測地系の雑学をお話しした通り、いろいろなやり方がありますが、ここでは、一般的なWGS84に則した方法をとりたいと思います。(単に、小職がこの方法しか知らないというのも理由の一つですが・・・)
とはいいながら、軌道計算もさることながら、経度、緯度に変換する方法はさらにその上をいって難しいです。よってこれもまともに解くとわけが分からなくなります。(少なくとも小職はそうです)
というわけで、ここでは、WGS84測地系の定義を以下のように簡素化します。
○座標系
ECEF系(ここは特に変更なしです。)
○準拠楕円体
楕円でなく真円とする。
○ジオイド面
高さは今回は意識しません。経度と緯度が求まればいいとします。
こんな感じです。実質、経度緯度を求めるという意味では、今回は楕円を真円と見なしているだけですが、実際は大問題です。しかしながら、だいたいこのへんと見るという前提で許してください。また、次ステップへの橋渡しと考えてください。
では、次から本格的に説明していきたいと思います。
尚、すでに、測地系の雑学をお話しした通り、いろいろなやり方がありますが、ここでは、一般的なWGS84に則した方法をとりたいと思います。(単に、小職がこの方法しか知らないというのも理由の一つですが・・・)
とはいいながら、軌道計算もさることながら、経度、緯度に変換する方法はさらにその上をいって難しいです。よってこれもまともに解くとわけが分からなくなります。(少なくとも小職はそうです)
というわけで、ここでは、WGS84測地系の定義を以下のように簡素化します。
○座標系
ECEF系(ここは特に変更なしです。)
○準拠楕円体
楕円でなく真円とする。
○ジオイド面
高さは今回は意識しません。経度と緯度が求まればいいとします。
こんな感じです。実質、経度緯度を求めるという意味では、今回は楕円を真円と見なしているだけですが、実際は大問題です。しかしながら、だいたいこのへんと見るという前提で許してください。また、次ステップへの橋渡しと考えてください。
では、次から本格的に説明していきたいと思います。
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

