GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
「航法メッセージによる GPS衛星の位置の求め方 其2」で2次元空間上でのGPS衛星の位置の求め方をお話いたしました。さてようやくですが、3次元空間上でのGPS衛星の位置を求めてみましょう。
まず、地球上のGPS受信機により、衛星位置は利用されますので、基準座標をGPS衛星の楕円軌道上の中心から地球の中心に移動させ、以下の図のようなイメージで座標空間を設定します。

図1
図1は地球を赤道面で真っ二つに割ったイメージで、赤道面中心から、春分点方向にx軸、赤道面中心から北極点方向にz軸をとります。この時、必然的にy軸方向は決定します。
さて、ここで、前回お話した、楕円上の衛星位置(x',y')を求める式を以下の通り、地球中心とした形に変更します。

数式1
これに関しては問題ないと思いますが、x'とy'とダッシュをつけたのは、3次元での軌道でのx,yとは異なるためです。
まずは次の図を見てください。

図2
なんかややこしい図がでてきましたが、まず頭をやわらかくして、聞いてください。図2に軌道面とあります。これは、GPS軌道の平面を表します。そして、この軌道面ですが、3次元上では、図のように、赤道面からみて傾いています。
ここまで、くるとなんとなく分かりますが、2次元上のGPS衛星の位置(x',y')について軌道面を斜めに向けた時の位置にしてやればいいわけです。
さて、3次元に座標を変換するための軌道パラメータが与えられていなければなんにもすることができませんので、ここで、簡単に航法メッセージより得られる軌道面に関する軌道パラメータを、紹介すると、
昇交点赤経Ω、軌道傾斜角i、近地点引数ωがあります。これはすべて角度をあらわし、図2に記述している通りで、これが決定すると軌道面の傾きがわかるわけです。とはいえ、なんかぴんとこないので、次のように考えると分かりやすいです。
「3次元の軌道面は、2次元の軌道面をz 軸回りにω 回転させ,続いてx 軸まわりにi,z 軸回りにΩ 回転させたものである」
こうすると感覚的にわかりますよね。よって回転行列を用いて、以下のようにGPS衛星の3次元座標上の位置(x,y,z)を求めることができます。

数式2
2次元面ではz軸は存在しませんので0になります。尚、ここでは回転行列の説明はしません。ただ、回転行列の概念は3Dをやる上では結構あそべるネタです。
一応、基本的な求め方はこれで終了なのですが、正確なGPS衛星の位置を計算するための軌道パラメータ要素は実際にはまだあり、これだけの計算では不十分と言えます。この話はまたの機会とします。
まず、地球上のGPS受信機により、衛星位置は利用されますので、基準座標をGPS衛星の楕円軌道上の中心から地球の中心に移動させ、以下の図のようなイメージで座標空間を設定します。
図1
図1は地球を赤道面で真っ二つに割ったイメージで、赤道面中心から、春分点方向にx軸、赤道面中心から北極点方向にz軸をとります。この時、必然的にy軸方向は決定します。
さて、ここで、前回お話した、楕円上の衛星位置(x',y')を求める式を以下の通り、地球中心とした形に変更します。
数式1
これに関しては問題ないと思いますが、x'とy'とダッシュをつけたのは、3次元での軌道でのx,yとは異なるためです。
まずは次の図を見てください。
図2
なんかややこしい図がでてきましたが、まず頭をやわらかくして、聞いてください。図2に軌道面とあります。これは、GPS軌道の平面を表します。そして、この軌道面ですが、3次元上では、図のように、赤道面からみて傾いています。
ここまで、くるとなんとなく分かりますが、2次元上のGPS衛星の位置(x',y')について軌道面を斜めに向けた時の位置にしてやればいいわけです。
さて、3次元に座標を変換するための軌道パラメータが与えられていなければなんにもすることができませんので、ここで、簡単に航法メッセージより得られる軌道面に関する軌道パラメータを、紹介すると、
昇交点赤経Ω、軌道傾斜角i、近地点引数ωがあります。これはすべて角度をあらわし、図2に記述している通りで、これが決定すると軌道面の傾きがわかるわけです。とはいえ、なんかぴんとこないので、次のように考えると分かりやすいです。
「3次元の軌道面は、2次元の軌道面をz 軸回りにω 回転させ,続いてx 軸まわりにi,z 軸回りにΩ 回転させたものである」
こうすると感覚的にわかりますよね。よって回転行列を用いて、以下のようにGPS衛星の3次元座標上の位置(x,y,z)を求めることができます。
数式2
2次元面ではz軸は存在しませんので0になります。尚、ここでは回転行列の説明はしません。ただ、回転行列の概念は3Dをやる上では結構あそべるネタです。
一応、基本的な求め方はこれで終了なのですが、正確なGPS衛星の位置を計算するための軌道パラメータ要素は実際にはまだあり、これだけの計算では不十分と言えます。この話はまたの機会とします。
PR
前回「航法メッセージによる GPS衛星の位置の求め方 其の1」で楕円に関する知識を学び、GPSの軌道計算するためには、時間の要素と媒介変数による楕円の公式の変換が必要であることを言いました。
さて、早速ですが、まず、楕円の公式を媒介変数表示させるために、まず以下の図を見てください。
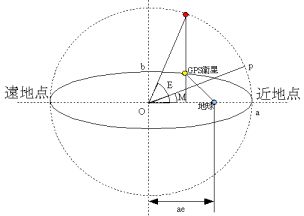
図1
まあ、前回に似た図ですが、なにやら怪しくなってきましたね。いろいろポイントはありますが、私は結構ここでつまづいてました。
図1のように、GPS衛星の軌道を表す楕円の長径(2a)に接するように真円を描きます。そして、GPS衛星から垂直に線を上方に伸ばし、真円とクロスする点から原点Oに直線を延ばします。この直線と、x軸が成す角をEとしこの角度を離心近点角と呼びます。こうすると、以下のように、楕円の公式を置き換えることができます。
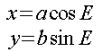
数式1
ここで、お分かりでしょうが、衛星位置(x,y)、aは長半径、bは短半径とします。これがいわゆる媒介変数表示という奴ですが、ようはどうにかして、位置を求めたいからいろいろ模索して、解が求めやすい形にしたわけです。
しかしながら、折角求めやすい形にしましたが、航法メッセージの軌道パラメータには短半径はなく、長半径しかありません、よって、何かしらこのbを変換してやる必要があります。
図1の地球に着目してください。地球と原点の距離をaeとしてます。ここでeは離心率とよばれ、地球が楕円の中心からどれだけ離れているかの度合いを表しているものです。ひとまず、このeと長半径を掛ければ、地球と原点との距離が求まるような離心率eを設定すると考えてください。この時、短半径bは次式で与えられます。
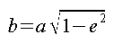
数式2
これで、bはどうにか回避しました、幸い離心率eは軌道パラメータに含まれているので利用できます。
さて、問題は観測時間における、離心近点角Eが求まらねば、衛星位置(x,y)は求まらないわけですが、まず短的に考えると、ある時間における、離心近点角Eと、衛星の地球を回る公転周期が分かれば、観測時の離心近点角Eがわかるような感じがします。しかしながら、これには大きな落とし穴があります。地球を回るGPS衛星の動きは一定でなく図1の近地点(楕円軌道で、地球にもっとも近い地点)あたりは早く動き、遠地点(楕円軌道で、地球から最も遠い地点)では遅くなるわけです。つまり、単純に計算できません。そこで、媒介変数とはいきませんが、一定の運動表現を用いねばなりません。
この時、図1を見ていただきたいのですが、Mという角度も記載しております。このMを決定ずける真円上の点pは真円における扇形 近地点 O pの面積が軌道楕円における扇形 近地点 地球 GPS衛星 の面積と楕円率(長半径 a と短半径 b の比 b/a)の逆数との積に等しくなるような円上の点にしております。ちょっとややこしい表現ですが、面積比を一定にしていると考えてください。
ここで、ケプラーの第2法則を持ち出します。第2法則は
「惑星と太陽とを結ぶ線分が単位時間に描く面積は、一定である」となっております。言い換えれば、
「GPS衛星と地球を結ぶ線分が単位時間に描く面積は、一定である」というわけです。角度は一定でないのですが、面積は一定であるということは、単位時間ごとにみれば、扇形 近地点 地球 GPS衛星の面積は一定の割合で増減していることになります。従って、近地点 O pの面積もまた、一定の割合で面積が増減することになります。ここでポイントは、近地点 O p の面積が一定ということは、真円ですので、角度Mは一定の割合で増減することになります。ここでMのことを、平均近点角と呼びます。
さて、実はこのMとEには一定の法則があります。これを、ケプラーの方程式といい、以下に示します。
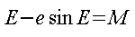
数式3
平均近点角Mは観測時での角度になりますので、まずは、軌道パラメータと現在時刻からそれを求めねばなりません。航法メッセージ内の軌道パラメータには、元期(軌道パラメータ更新時)の平均近点角M0が含まれますので、これで、初期の、角度は求まります。あとは図1の点pの平均運動(1日あたりの回転数)がわかれば、元期から観測時までの時間差によりどれだけ基準から回転したかがわかりますので、必然的に観測時の平均近点角Mが求まるわけです。
尚、この平均運動ですが、ケプラーの第3法則を利用し算出します。ケプラーの第3法則は
「惑星の公転周期の2乗は、軌道の長半径の3乗に比例する。」
というものです。いやはやすごいですね、先人に感謝です。また、あの有名なニュートンはこの第3法則と万有引力とに関係があることを導き出しました。
この時、軌道長半径を a、公転周期をT、主星の質量をM 、伴星の質量をm、万有引力定数をGとすれば
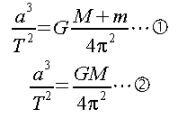
数式4
数式4の①が成り立ちます。ただし、今回の場合は、伴星はGPS衛星ですので、質量が地球と対比して非常に小さいので0と見なし、一般的には②の方を利用します。
尚、Mを地球の質量として、GM = 3986005×108 程度で、航法パラメータにはありませんが、固定値としてGPS受信機内部に記憶されています。
これで、GPS衛星の平均運動を求めることができます。
いかがでしたでしょうか?、まだ2次元でのGPS衛星の軌道の話ですが、私的にはかなりしんどいです。この記事書くのに、10時間もかかった・・・。しかも、公式の導き出し方も結構はしょってるので、これわこれで、またの機会にやっていきます。
とりあえず今日はここまで。
さて、早速ですが、まず、楕円の公式を媒介変数表示させるために、まず以下の図を見てください。
図1
まあ、前回に似た図ですが、なにやら怪しくなってきましたね。いろいろポイントはありますが、私は結構ここでつまづいてました。
図1のように、GPS衛星の軌道を表す楕円の長径(2a)に接するように真円を描きます。そして、GPS衛星から垂直に線を上方に伸ばし、真円とクロスする点から原点Oに直線を延ばします。この直線と、x軸が成す角をEとしこの角度を離心近点角と呼びます。こうすると、以下のように、楕円の公式を置き換えることができます。
数式1
ここで、お分かりでしょうが、衛星位置(x,y)、aは長半径、bは短半径とします。これがいわゆる媒介変数表示という奴ですが、ようはどうにかして、位置を求めたいからいろいろ模索して、解が求めやすい形にしたわけです。
しかしながら、折角求めやすい形にしましたが、航法メッセージの軌道パラメータには短半径はなく、長半径しかありません、よって、何かしらこのbを変換してやる必要があります。
図1の地球に着目してください。地球と原点の距離をaeとしてます。ここでeは離心率とよばれ、地球が楕円の中心からどれだけ離れているかの度合いを表しているものです。ひとまず、このeと長半径を掛ければ、地球と原点との距離が求まるような離心率eを設定すると考えてください。この時、短半径bは次式で与えられます。
数式2
これで、bはどうにか回避しました、幸い離心率eは軌道パラメータに含まれているので利用できます。
さて、問題は観測時間における、離心近点角Eが求まらねば、衛星位置(x,y)は求まらないわけですが、まず短的に考えると、ある時間における、離心近点角Eと、衛星の地球を回る公転周期が分かれば、観測時の離心近点角Eがわかるような感じがします。しかしながら、これには大きな落とし穴があります。地球を回るGPS衛星の動きは一定でなく図1の近地点(楕円軌道で、地球にもっとも近い地点)あたりは早く動き、遠地点(楕円軌道で、地球から最も遠い地点)では遅くなるわけです。つまり、単純に計算できません。そこで、媒介変数とはいきませんが、一定の運動表現を用いねばなりません。
この時、図1を見ていただきたいのですが、Mという角度も記載しております。このMを決定ずける真円上の点pは真円における扇形 近地点 O pの面積が軌道楕円における扇形 近地点 地球 GPS衛星 の面積と楕円率(長半径 a と短半径 b の比 b/a)の逆数との積に等しくなるような円上の点にしております。ちょっとややこしい表現ですが、面積比を一定にしていると考えてください。
ここで、ケプラーの第2法則を持ち出します。第2法則は
「惑星と太陽とを結ぶ線分が単位時間に描く面積は、一定である」となっております。言い換えれば、
「GPS衛星と地球を結ぶ線分が単位時間に描く面積は、一定である」というわけです。角度は一定でないのですが、面積は一定であるということは、単位時間ごとにみれば、扇形 近地点 地球 GPS衛星の面積は一定の割合で増減していることになります。従って、近地点 O pの面積もまた、一定の割合で面積が増減することになります。ここでポイントは、近地点 O p の面積が一定ということは、真円ですので、角度Mは一定の割合で増減することになります。ここでMのことを、平均近点角と呼びます。
さて、実はこのMとEには一定の法則があります。これを、ケプラーの方程式といい、以下に示します。
数式3
平均近点角Mは観測時での角度になりますので、まずは、軌道パラメータと現在時刻からそれを求めねばなりません。航法メッセージ内の軌道パラメータには、元期(軌道パラメータ更新時)の平均近点角M0が含まれますので、これで、初期の、角度は求まります。あとは図1の点pの平均運動(1日あたりの回転数)がわかれば、元期から観測時までの時間差によりどれだけ基準から回転したかがわかりますので、必然的に観測時の平均近点角Mが求まるわけです。
尚、この平均運動ですが、ケプラーの第3法則を利用し算出します。ケプラーの第3法則は
「惑星の公転周期の2乗は、軌道の長半径の3乗に比例する。」
というものです。いやはやすごいですね、先人に感謝です。また、あの有名なニュートンはこの第3法則と万有引力とに関係があることを導き出しました。
この時、軌道長半径を a、公転周期をT、主星の質量をM 、伴星の質量をm、万有引力定数をGとすれば
数式4
数式4の①が成り立ちます。ただし、今回の場合は、伴星はGPS衛星ですので、質量が地球と対比して非常に小さいので0と見なし、一般的には②の方を利用します。
尚、Mを地球の質量として、GM = 3986005×108 程度で、航法パラメータにはありませんが、固定値としてGPS受信機内部に記憶されています。
これで、GPS衛星の平均運動を求めることができます。
いかがでしたでしょうか?、まだ2次元でのGPS衛星の軌道の話ですが、私的にはかなりしんどいです。この記事書くのに、10時間もかかった・・・。しかも、公式の導き出し方も結構はしょってるので、これわこれで、またの機会にやっていきます。
とりあえず今日はここまで。
前回、「GPS受信機の位置計算」で、GPSによる位置の測位概念を記載しました。さて、いよいよ、航法メッセージのGPS衛星の軌道パラメータからGPS衛星の位置をGPS受信機が知る方法を学んでいきたいと思います。
といっても、最初っから、航法メッセージのパラメータ情報で公式を用いて、算出させるには、あまりにも敷居が高いので、基礎的なところをまずは数回に分けて解説したいと思います。正直、この辺にくると、公式のオンパレードで私自身、説明が危ぶまれますが、ともかく気長に行きましょう。
さて、GPS衛星にかかわらず人工衛星は地球の周りを楕円を描きながら、回っております。別に狙ってうごいているのではなく、物理法則に従い、動かされています。ここはポイントです。
これは、1619年にヨハネスケプラーによって、解明された「惑星は、太陽をひとつの焦点とする楕円軌道上を動く。」という原理の基、GPS衛星の運動も楕円運動になります。衛星と呼ばれるのもなっとくいきます。
ここで、少し、楕円について勉強しましょう。
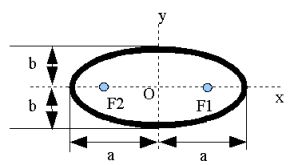
図1
まず、図1をみてください。楕円の軌跡は「平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線」です。図1でいくとこの2定点はF1、F2となり、F1とF2はY軸で対象となってます。F1=F2の場合は原点Oに重なりますから、この場合は楕円でなく真円になります。
ここで、図1のaの部分は楕円で一番長い半径なので、長半径、bの部分は一番短い半径なので、短半径と言い、これを利用し、楕円の公式は
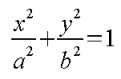
数式1
として表せます。ここではこの証明は省きます。
楕円の基礎知識はなんとなくわかりましたでしょうか?実は、GPS衛星の動きもこれに当てはめることができ、図1で言えば、F1を地球、楕円を描きまわっているのがGPS衛星と置き換えても実は成り立つのです。
正直、すごく不思議な気がします。GPS衛星が地球の周りを楕円を描きながら、回っているのは、ボールをどんどん遠くに飛ばしていくイメージを頭に浮かべると、なーんとなくわかるような気にはなりますが、それが楕円の公式と結びつくのがいまいちピントこないわけです。しかしながら、楕円の定義を頭で思い浮かべ、楕円を描くアニメーションをイメージするとなんとなく分かった気持ちにもなります。みんさんもイメージしてみてください・・・。
さてさて、今までの知識を使って、3次元空間でのGPS衛星の位置は後回しにして、2次元空間のGPS衛星の位置(x,y)を考えて見ましょう。ある時間において、現在、GPS衛星は2次元座標のどこにあるか?を知りたいとします。さて、数式1を使って・・・・。もうお分かりと思いますが、数式1ではどうしようもありません。そもそも時間の要素が何もはいってないので・・・。
というわけで何かしら時間の要素を与えないといけないですね。それと、x,y座標の位置を求めるためには、GPS受信機の位置を求めたように連立方程式をつかう?これは無理ですよね、なんせ、軌道要素は1パターンしかありませんので、ここで、登場するのが媒介変数表示というやつです。ここまでくるとなにが何やらですね。これ以上やると長くなるので、ここでいったん切ります。
といっても、最初っから、航法メッセージのパラメータ情報で公式を用いて、算出させるには、あまりにも敷居が高いので、基礎的なところをまずは数回に分けて解説したいと思います。正直、この辺にくると、公式のオンパレードで私自身、説明が危ぶまれますが、ともかく気長に行きましょう。
さて、GPS衛星にかかわらず人工衛星は地球の周りを楕円を描きながら、回っております。別に狙ってうごいているのではなく、物理法則に従い、動かされています。ここはポイントです。
これは、1619年にヨハネスケプラーによって、解明された「惑星は、太陽をひとつの焦点とする楕円軌道上を動く。」という原理の基、GPS衛星の運動も楕円運動になります。衛星と呼ばれるのもなっとくいきます。
ここで、少し、楕円について勉強しましょう。
図1
まず、図1をみてください。楕円の軌跡は「平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線」です。図1でいくとこの2定点はF1、F2となり、F1とF2はY軸で対象となってます。F1=F2の場合は原点Oに重なりますから、この場合は楕円でなく真円になります。
ここで、図1のaの部分は楕円で一番長い半径なので、長半径、bの部分は一番短い半径なので、短半径と言い、これを利用し、楕円の公式は
数式1
として表せます。ここではこの証明は省きます。
楕円の基礎知識はなんとなくわかりましたでしょうか?実は、GPS衛星の動きもこれに当てはめることができ、図1で言えば、F1を地球、楕円を描きまわっているのがGPS衛星と置き換えても実は成り立つのです。
正直、すごく不思議な気がします。GPS衛星が地球の周りを楕円を描きながら、回っているのは、ボールをどんどん遠くに飛ばしていくイメージを頭に浮かべると、なーんとなくわかるような気にはなりますが、それが楕円の公式と結びつくのがいまいちピントこないわけです。しかしながら、楕円の定義を頭で思い浮かべ、楕円を描くアニメーションをイメージするとなんとなく分かった気持ちにもなります。みんさんもイメージしてみてください・・・。
さてさて、今までの知識を使って、3次元空間でのGPS衛星の位置は後回しにして、2次元空間のGPS衛星の位置(x,y)を考えて見ましょう。ある時間において、現在、GPS衛星は2次元座標のどこにあるか?を知りたいとします。さて、数式1を使って・・・・。もうお分かりと思いますが、数式1ではどうしようもありません。そもそも時間の要素が何もはいってないので・・・。
というわけで何かしら時間の要素を与えないといけないですね。それと、x,y座標の位置を求めるためには、GPS受信機の位置を求めたように連立方程式をつかう?これは無理ですよね、なんせ、軌道要素は1パターンしかありませんので、ここで、登場するのが媒介変数表示というやつです。ここまでくるとなにが何やらですね。これ以上やると長くなるので、ここでいったん切ります。
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

