GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回、「GPS受信機の位置計算」で、GPSによる位置の測位概念を記載しました。さて、いよいよ、航法メッセージのGPS衛星の軌道パラメータからGPS衛星の位置をGPS受信機が知る方法を学んでいきたいと思います。
といっても、最初っから、航法メッセージのパラメータ情報で公式を用いて、算出させるには、あまりにも敷居が高いので、基礎的なところをまずは数回に分けて解説したいと思います。正直、この辺にくると、公式のオンパレードで私自身、説明が危ぶまれますが、ともかく気長に行きましょう。
さて、GPS衛星にかかわらず人工衛星は地球の周りを楕円を描きながら、回っております。別に狙ってうごいているのではなく、物理法則に従い、動かされています。ここはポイントです。
これは、1619年にヨハネスケプラーによって、解明された「惑星は、太陽をひとつの焦点とする楕円軌道上を動く。」という原理の基、GPS衛星の運動も楕円運動になります。衛星と呼ばれるのもなっとくいきます。
ここで、少し、楕円について勉強しましょう。
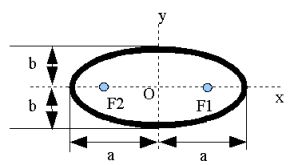
図1
まず、図1をみてください。楕円の軌跡は「平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線」です。図1でいくとこの2定点はF1、F2となり、F1とF2はY軸で対象となってます。F1=F2の場合は原点Oに重なりますから、この場合は楕円でなく真円になります。
ここで、図1のaの部分は楕円で一番長い半径なので、長半径、bの部分は一番短い半径なので、短半径と言い、これを利用し、楕円の公式は
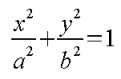
数式1
として表せます。ここではこの証明は省きます。
楕円の基礎知識はなんとなくわかりましたでしょうか?実は、GPS衛星の動きもこれに当てはめることができ、図1で言えば、F1を地球、楕円を描きまわっているのがGPS衛星と置き換えても実は成り立つのです。
正直、すごく不思議な気がします。GPS衛星が地球の周りを楕円を描きながら、回っているのは、ボールをどんどん遠くに飛ばしていくイメージを頭に浮かべると、なーんとなくわかるような気にはなりますが、それが楕円の公式と結びつくのがいまいちピントこないわけです。しかしながら、楕円の定義を頭で思い浮かべ、楕円を描くアニメーションをイメージするとなんとなく分かった気持ちにもなります。みんさんもイメージしてみてください・・・。
さてさて、今までの知識を使って、3次元空間でのGPS衛星の位置は後回しにして、2次元空間のGPS衛星の位置(x,y)を考えて見ましょう。ある時間において、現在、GPS衛星は2次元座標のどこにあるか?を知りたいとします。さて、数式1を使って・・・・。もうお分かりと思いますが、数式1ではどうしようもありません。そもそも時間の要素が何もはいってないので・・・。
というわけで何かしら時間の要素を与えないといけないですね。それと、x,y座標の位置を求めるためには、GPS受信機の位置を求めたように連立方程式をつかう?これは無理ですよね、なんせ、軌道要素は1パターンしかありませんので、ここで、登場するのが媒介変数表示というやつです。ここまでくるとなにが何やらですね。これ以上やると長くなるので、ここでいったん切ります。
といっても、最初っから、航法メッセージのパラメータ情報で公式を用いて、算出させるには、あまりにも敷居が高いので、基礎的なところをまずは数回に分けて解説したいと思います。正直、この辺にくると、公式のオンパレードで私自身、説明が危ぶまれますが、ともかく気長に行きましょう。
さて、GPS衛星にかかわらず人工衛星は地球の周りを楕円を描きながら、回っております。別に狙ってうごいているのではなく、物理法則に従い、動かされています。ここはポイントです。
これは、1619年にヨハネスケプラーによって、解明された「惑星は、太陽をひとつの焦点とする楕円軌道上を動く。」という原理の基、GPS衛星の運動も楕円運動になります。衛星と呼ばれるのもなっとくいきます。
ここで、少し、楕円について勉強しましょう。
図1
まず、図1をみてください。楕円の軌跡は「平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線」です。図1でいくとこの2定点はF1、F2となり、F1とF2はY軸で対象となってます。F1=F2の場合は原点Oに重なりますから、この場合は楕円でなく真円になります。
ここで、図1のaの部分は楕円で一番長い半径なので、長半径、bの部分は一番短い半径なので、短半径と言い、これを利用し、楕円の公式は
数式1
として表せます。ここではこの証明は省きます。
楕円の基礎知識はなんとなくわかりましたでしょうか?実は、GPS衛星の動きもこれに当てはめることができ、図1で言えば、F1を地球、楕円を描きまわっているのがGPS衛星と置き換えても実は成り立つのです。
正直、すごく不思議な気がします。GPS衛星が地球の周りを楕円を描きながら、回っているのは、ボールをどんどん遠くに飛ばしていくイメージを頭に浮かべると、なーんとなくわかるような気にはなりますが、それが楕円の公式と結びつくのがいまいちピントこないわけです。しかしながら、楕円の定義を頭で思い浮かべ、楕円を描くアニメーションをイメージするとなんとなく分かった気持ちにもなります。みんさんもイメージしてみてください・・・。
さてさて、今までの知識を使って、3次元空間でのGPS衛星の位置は後回しにして、2次元空間のGPS衛星の位置(x,y)を考えて見ましょう。ある時間において、現在、GPS衛星は2次元座標のどこにあるか?を知りたいとします。さて、数式1を使って・・・・。もうお分かりと思いますが、数式1ではどうしようもありません。そもそも時間の要素が何もはいってないので・・・。
というわけで何かしら時間の要素を与えないといけないですね。それと、x,y座標の位置を求めるためには、GPS受信機の位置を求めたように連立方程式をつかう?これは無理ですよね、なんせ、軌道要素は1パターンしかありませんので、ここで、登場するのが媒介変数表示というやつです。ここまでくるとなにが何やらですね。これ以上やると長くなるので、ここでいったん切ります。
PR
この記事にコメントする
カレンダー
| 03 | 2025/04 | 05 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

