GPS関連の話題を掲載していきます。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回「航法メッセージによる GPS衛星の位置の求め方 其の3」で航法メッセージからGPS衛星の位置を求める概念をお話いたしました。さて、ここでは、航法メッセージの中に含まれるアルマナックデータを利用して、実際にGPS衛星の位置を計算したいと思います。
まずは、なるべく新しいアルマナックデータを取ってくる必要があるのですが、これは、米国政府が運用している、ナビゲーションセンターのサイトから入手可能です。
また、今回はまだ運用が開始していませんが、折角ですので、5月28日に打ち上げられた、ブロックIIFシリーズのGPS衛星の位置を計算してみます。
取得したアルマナックデータの内容は以下の通りになります。ついでに、変数も定義しておきます。
数字をみるとなにやら気分が悪くなりそうですね。前回の概念があれば、なんとなくは分かると思います。
計算に入る前に捕捉すると、IDはGPS衛星の番号です。そして、HEALTHは健康状態で、000以外の数字が入っていれば、利用不可能です。今回はまだ運用が始まってませんので、000以外の値が入っております。また、a0,a1は位置計算では利用しません。これは、受信機の内部時計の補正等に利用します。
さて、ここから本格的に計算を始めますが、まずは下ごしらえをします。計算に使う材料を計算させるとでも思ってください。
まず、平均運動N0を求めます。単位時間あたりにどれだけ衛星が地球を公転するかがこれを求めればわかります。これを求めるには、ケプラーの第3法則とニュートンの公式から、
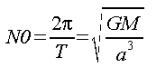
と表すことができますので、GMは前回お話したとおり、既知でGM = 398600500000000、aはアルマナックデータの二乗で a = 26840266.686221562
になり、N0 = 0.00014357825789904194となります。
次が重要ですが、アルマナックデータが生成された、基準時刻と、GPS衛星の位置を求める時刻との差を求めます。これがないとはじまりませんよね。
まず、アルマナックデータが生成された基準時刻を求めますが、これはアルマナックデータのtaとWEEKを用います。
WEEKは、1980年1月6日0時0分0秒(UTC)を第0週として、取得したアルマナックデータを生成されたのが第何週目にあたるかを表しており、taはその週を基準とし、何秒後にアルマナックデータが生成されたかを表しております。
1980年ってのはGPSの運用の始まりと推測はつくと思います。ちなみにこの時点では4基のGPS衛星しか存在してなかったようです。
さて、ここまで言えば、時間差は容易にもとまるといいたいところですが、WEEKをよく見てください。どうみても、1980年からのWEEKにしては少なすぎます。実は、古い、GPS衛星のWEEK用のカウンターは10ビットつまり、1023までしかカウントできなかったため、1999年8月22日に1度リセットがかかっているためです。これは俗にゆう2000年問題の一つだったようです。ここらへんの対策はすでに、カーナビ等には備わっていたのか、問題はさほどでなかったようです。新しいGPS衛星では問題ないのでしょうが、今更、これを変更させるわけにもいかないので、今後どのようになるのか見ものです。
さて、というわけで、実際のWEEKは1024 + 564になります。
よって、1980年1月6日0時0分0秒からアルマナックデータ更新までの通算時刻(基準時刻(s))は
(7.0 * 24.0 * 60.0 * 60.0) * (1024 + 564) + 61440秒となります。
したがって、1980年1月6日0時0分0秒から現在の時刻(衛星の位置を求める時刻)の通算秒からこれを引けば、アルマナック生成の基準時刻からどれだけの秒数がたったのか分かります。ここで、(1980年1月6日0:0:0から現時点までの通算秒) - ((7.0 * 24.0 * 60.0 * 60.0) * (1024 + 564) + 61440) = 503490 = tkとします。
だいぶ材料がそろってきました。
さて、ここで、ようやく、現在時刻における、平均近点角を求めることができます。平均近点角Mは、以下の通り求めることができます。
M = M0 + tk * N0
M = 1.111893773 + 503490* 0.00014357825789904194 = 73.40211084258863
ここでM0はアルマナックデータより得られる。アルマナックデータ生成時の平均近点角ですので、そこを基準にどれだけ回転したかを求めるだけですので、いたってシンプルですよね。
さて、この時点で昇交点経度も求めておきます。残念ながら、昇交点経度も時間とともに変化しますのでこれも必須です。考え方は平均近点角の求め方と同様で、現在時刻による昇交点経度をΩKとすれば、
ΩK = ℓ0 + tk * Ω・dot
で求めることができます。したがって、Ωk = -3.115975261 + 503490 * -0.7425114745e-8 = -3.11971373202296
となります。
これで、仕込みは完了です。次回は、ケプラーの方程式等を用いて、本格的な計算をします。
まずは、なるべく新しいアルマナックデータを取ってくる必要があるのですが、これは、米国政府が運用している、ナビゲーションセンターのサイトから入手可能です。
また、今回はまだ運用が開始していませんが、折角ですので、5月28日に打ち上げられた、ブロックIIFシリーズのGPS衛星の位置を計算してみます。
取得したアルマナックデータの内容は以下の通りになります。ついでに、変数も定義しておきます。
| 変数 | 意味 | 値 |
| ID | 衛星のPRN 番号 | 25 |
| HEALTH | 衛星の健康状態(000 の場合は利用可能) | 063 |
| e | 軌道離心率 | 0.9350776672e-3 |
| ta | 現GPS週におけるalmanac軌道要素の基準時刻(s) | 61440 |
| i | 軌道傾斜角(rad) | 0.9600639343 |
| Ω ⋅ dot | 昇交点経度の変化率(rad/s) | -0.7425114745e-8 |
| √a | 軌道長半径の平方根 | 5180.759277 |
| ℓ0 | 基準時刻における昇交点経度(rad) | -0.3115975261e+1 |
| ω | 近地点引数(rad) | 2.185029387 |
| M0 | 基準時刻taにおける平均近点離角(rad) | 0.1111893773e+1 |
| a0 | 時計の位相バイアス(s) | 0.9536743164e-6 |
| a1 | 時計の周波数バイアス(s/s) | 0.0000000000e+0 |
| WEEK | GPS 週 | 564 |
数字をみるとなにやら気分が悪くなりそうですね。前回の概念があれば、なんとなくは分かると思います。
計算に入る前に捕捉すると、IDはGPS衛星の番号です。そして、HEALTHは健康状態で、000以外の数字が入っていれば、利用不可能です。今回はまだ運用が始まってませんので、000以外の値が入っております。また、a0,a1は位置計算では利用しません。これは、受信機の内部時計の補正等に利用します。
さて、ここから本格的に計算を始めますが、まずは下ごしらえをします。計算に使う材料を計算させるとでも思ってください。
まず、平均運動N0を求めます。単位時間あたりにどれだけ衛星が地球を公転するかがこれを求めればわかります。これを求めるには、ケプラーの第3法則とニュートンの公式から、
と表すことができますので、GMは前回お話したとおり、既知でGM = 398600500000000、aはアルマナックデータの二乗で a = 26840266.686221562
になり、N0 = 0.00014357825789904194となります。
次が重要ですが、アルマナックデータが生成された、基準時刻と、GPS衛星の位置を求める時刻との差を求めます。これがないとはじまりませんよね。
まず、アルマナックデータが生成された基準時刻を求めますが、これはアルマナックデータのtaとWEEKを用います。
WEEKは、1980年1月6日0時0分0秒(UTC)を第0週として、取得したアルマナックデータを生成されたのが第何週目にあたるかを表しており、taはその週を基準とし、何秒後にアルマナックデータが生成されたかを表しております。
1980年ってのはGPSの運用の始まりと推測はつくと思います。ちなみにこの時点では4基のGPS衛星しか存在してなかったようです。
さて、ここまで言えば、時間差は容易にもとまるといいたいところですが、WEEKをよく見てください。どうみても、1980年からのWEEKにしては少なすぎます。実は、古い、GPS衛星のWEEK用のカウンターは10ビットつまり、1023までしかカウントできなかったため、1999年8月22日に1度リセットがかかっているためです。これは俗にゆう2000年問題の一つだったようです。ここらへんの対策はすでに、カーナビ等には備わっていたのか、問題はさほどでなかったようです。新しいGPS衛星では問題ないのでしょうが、今更、これを変更させるわけにもいかないので、今後どのようになるのか見ものです。
さて、というわけで、実際のWEEKは1024 + 564になります。
よって、1980年1月6日0時0分0秒からアルマナックデータ更新までの通算時刻(基準時刻(s))は
(7.0 * 24.0 * 60.0 * 60.0) * (1024 + 564) + 61440秒となります。
したがって、1980年1月6日0時0分0秒から現在の時刻(衛星の位置を求める時刻)の通算秒からこれを引けば、アルマナック生成の基準時刻からどれだけの秒数がたったのか分かります。ここで、(1980年1月6日0:0:0から現時点までの通算秒) - ((7.0 * 24.0 * 60.0 * 60.0) * (1024 + 564) + 61440) = 503490 = tkとします。
だいぶ材料がそろってきました。
さて、ここで、ようやく、現在時刻における、平均近点角を求めることができます。平均近点角Mは、以下の通り求めることができます。
M = M0 + tk * N0
M = 1.111893773 + 503490* 0.00014357825789904194 = 73.40211084258863
ここでM0はアルマナックデータより得られる。アルマナックデータ生成時の平均近点角ですので、そこを基準にどれだけ回転したかを求めるだけですので、いたってシンプルですよね。
さて、この時点で昇交点経度も求めておきます。残念ながら、昇交点経度も時間とともに変化しますのでこれも必須です。考え方は平均近点角の求め方と同様で、現在時刻による昇交点経度をΩKとすれば、
ΩK = ℓ0 + tk * Ω・dot
で求めることができます。したがって、Ωk = -3.115975261 + 503490 * -0.7425114745e-8 = -3.11971373202296
となります。
これで、仕込みは完了です。次回は、ケプラーの方程式等を用いて、本格的な計算をします。
PR
この記事にコメントする
カレンダー
| 01 | 2026/02 | 03 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
カテゴリー
フリーエリア
最新コメント
最新記事
(01/29)
(01/06)
(11/23)
(11/21)
(10/10)
(10/10)
(09/12)
(08/04)
(08/03)
(07/31)
最新トラックバック
プロフィール
HN:
Slit
性別:
非公開
ブログ内検索
最古記事
(05/12)
(05/13)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/18)
(05/18)
(05/19)
アクセス解析

